⚠️THIS NOTE IS NOT FINISHED YET
TODO:
- stirling number definitions
- stirling number of the first and the second type
- bell number
Question
Can you find a closed formula for the sum of the $p$-th powers of the first $n$ positive integers? That is, we need a closed formulat for the sequence:
$$ h_n=a_p n^p+a_{p-1} n^{p-1}+\cdots+a_1 n+a_0, \quad(n \geq 0) $$
Solution
The method is to use difference sequences. We already know the following:
$$ 1^3 + 2^3 + \ldots + n^3 = (1+2+\ldots + n)^2 $$ Now we want a new method. First, construct a difference table for $n^3$.
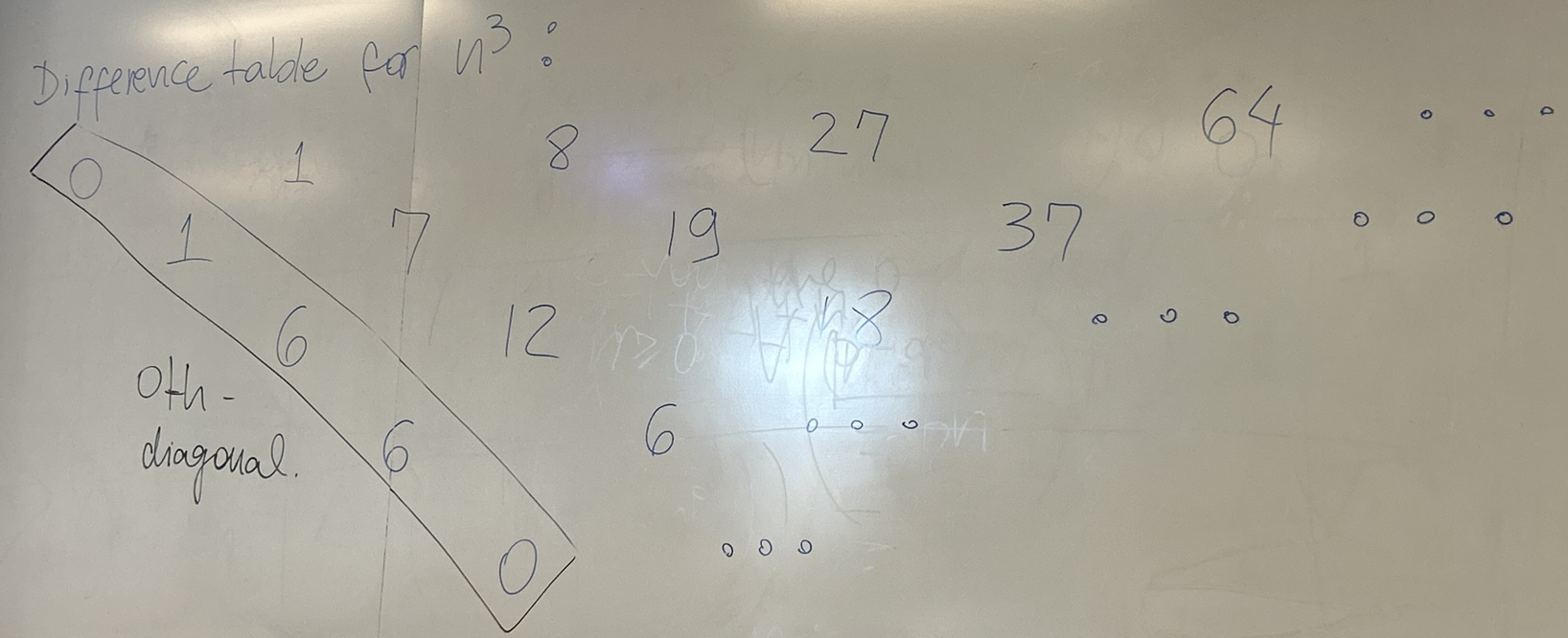
Let’s verify the following equation:
$$ 1^3 + \ldots + n^3 = 0 \cdot \binom{n+1}{1} + 1 \cdot \binom{n+1}{2} + 6 \cdot \binom{n+1}{3} + 6 \cdot \binom{n+1}{4} $$
Use Pascal’s formula for the last two terms. Then expand them to verify that this equation is true.
Definition
Let $(h_n)_{n \geq 0}$ be a sequence of numbers. We define a new sequence:
$$ \Delta h_0, \Delta h_1, \Delta h_2, \ldots, \Delta h_n, \ldots $$ call the first-order difference sequence of $(h_n)_{n \geq 0}$ by:
$$ \Delta h_n = h_{n+1} - h_n $$
Discrete derivative.
Definition
The second-order difference sequence of $(h_n)_{n \ge 0}$ is defined by
$$ \Delta^2 h_0, \Delta^2 h_1, \Delta^2 h_2, \ldots, \Delta^2 h_n, \ldots, $$ where
$$ \Delta^2 h_n = \Delta(\Delta h_n) = \Delta h_{n+1} - \Delta h_{n}. $$
Then we can construct the difference table using this new notation:
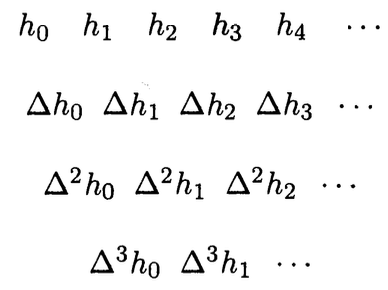
Theorem 8.2.1
Let the general term of a sequence be a polynomial of degree $p$ in $n$: $$ h_n = a_pn^p + a_{p-1}n^{p-1} + \ldots + a_1n + a_0, \quad(n\geq 0) $$ Then, $\Delta^{p+1} h_n = 0$ for all $n \geq 0$.
Proof
Induction on $p$. IH:
$$ \Delta^{p+1}h_n = 0, \forall n \geq 0, \forall p \text{-degree sequence } (h_n)_{n\geq 0} $$
Base case: $p = 0$, then $(h_n)_{n \geq 0}$ is a constant sequence $\implies \Delta h_n = h_{n+1} - h_n = 0$.
Induction step: Assume this holds for $p-1, p \geq 1$. Let’s show that this holds for $p$ as well. We have:
$$ \begin{align*} \Delta h_n = h_{n+1} - h_n &= \left(a_p(n+1)^p+a_{p-1}(n+1)^{p-1}+\cdots+a_1 n+a_0\right)\\ & \quad -\left(a_p n^p+a_{p-1} n^{p-1}+\cdots+a_1 n+a_0\right)\\ &= (a_p(n+1)^p - a_p n^p) + \text{polynomial with degree }p-1 \end{align*} $$
By IH, the polynomial with degree $p-1$ goes to zero. Since we want to show that $\Delta^{p+1} h_n$ still goes to zero, we need to show that:
$$ a_p(n+1)^p - a_p n^p = 0 $$
Now, to solve this, we can use binomial theorm:
$$ \begin{align*} a_p(n+1)^p - a_p n^p &= a_p\left( \sum_{i=0}^{p}\binom{p}{i}n^{i} \right) - a_pn^p\\ &= a_p\left( \sum_{i=0}^{p-1} \binom{p}{i}n^i \right) + a_p n^p - a_pn^p\\ &= a_p\left( \sum_{i=0}^{p-1} \binom{p}{i}n^i \right) \end{align*} $$
Which means that this polynomial also has degree $p-1$. Combining with the term above, we have: $$ \Delta ^{p+1} = \Delta^p(\Delta h_n) = \Delta^p(\text{Polynomial with degree }p-1) = 0 $$ $\blacksquare$
Lemma Linearity of difference
Let $(f_n)_{n\geq 0}$ and $(g_n)_{n\geq 0}$ be two sequences of numbers. Let $(h_n)_{n\geq 0}$ be a sequence defined by: $$ h_n = g_n + f_n $$ For every $p \geq 0$ we have: $$ \Delta^p h_n = \Delta^p g_n + \Delta^p f_n $$ Proof
It suffices to show that: $$ \Delta (f_n + g_n) = \Delta f_n + \Delta g_n $$ Expand this and use commutative property to show this:
$$ \begin{align*} \Delta h_n &=h_{n+1}-h_n \\ &=\left(g_{n+1}+f_{n+1}\right)-\left(g_n+f_n\right) \\ &=\left(g_{n+1}-g_n\right)+\left(f_{n+1}-f_n\right) \\ &=\Delta g_n+\Delta f_n \end{align*} $$
Question
Can we recover a sequence by knowing the $0^{\text{th}}$ diagonal of its difference table?
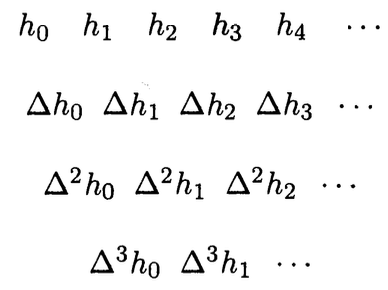
Note that the $0-$diagonal has the terms: $$ \Delta^0 h_0, \Delta^1 h_0, \Delta^2 h_0, \Delta^3 h_0, \ldots $$
Lemma
The general term of the sequence $\left(h_n\right)_{n \geq 0}$ such that the Oth diagonal of its difference table is
$$ \underbrace{000 \cdots 0}_{p \text { zeros }} 1000 \cdots $$ equals to
$$ h_n= \binom{n}{p} $$ Proof
From the 0-diagonal, we can first try to recover the 1-diagonal, 2-diagonal… and so on:
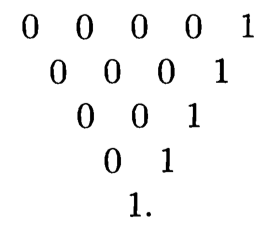
Say the $1$ is the fifth number to appear in the 0-diagonal, then it also appears at the fifth position in the first row. All the other terms in the first row are zero. We are then looking for a sequence that has the following properties: $$ h_0 = h_1 = h_2 = h_3 = h_4 = 0, h_1 = 1, $$ Thus, if $h_n$ is sequence of degree 4, it has roots at $0, 1, 2, 3$. Write out out simple guess, we have: $$ h_n = c \cdot n \cdot (n-1) \cdot (n-2) \cdot (n-3) $$ for some constant $c$. To satisfies the term $h_1 = 1$, $c = \frac{1}{4!}$. We discover that $h_n = \binom{n}{4}$. More generally, $h_n = \binom{n}{p}$ if there are $p$ zeros in the beginning of the 0-diagonal.
Intuition: using the linearity property of differences and the fact that the 0th diagonal of a difference table determines the entire difference table, and hence the sequence itself, we obtain the next theorem.
Theorem 8.2.2
The general term of the sequence whose difference table has its 0th diagonal equal to $$ c_0, c_1, c_2, \ldots, c_p, 0,0,0, \ldots, \quad \text { where } c_p \neq 0 $$ is a polynomial in $n$ of degree $p$ satisfying $$ h_n=c_0\left(\begin{array}{l} n \ 0 \end{array}\right)+c_1\left(\begin{array}{l} n \ 1 \end{array}\right)+c_2\left(\begin{array}{l} n \ 2 \end{array}\right)+\cdots+c_p\left(\begin{array}{l} n \ p \end{array}\right) $$
Now, we can back to the initial question: can we find a closed formula for the sum of the $p$-th powers of the first $n$ positive integers? Now we have the tools.
We can first write out the difference table. Then, we look at the 0-diagonal, and we reconstruct the sequence, but in the form we see in Theorem 8.2.2. Here is an example:
Exercise
Consider the sequence with general term $$ h_n=n^3+3 n^2-2 n+1, \quad(n \geq 0) $$ The 0-diagonal is $1,2,12,6,0,0, \ldots$. By using Theorem 8.2.2, we get: $$ h_n = \binom{n}{0} + 2\binom{n}{1} +12\binom{n}{2} + 6\binom{n}{3} $$ Summing them up: $$ \sum_{k=0}^{n} h_k = \sum_{k=0}^{n}\binom{k}{0} + 2\sum_{k=0}^{n}\binom{k}{1} +12\sum_{k=0}^{n}\binom{k}{2} + \sum_{k=0}^{n}6\binom{k}{3} $$ By hokey-stick identity, this turns to: $$ \sum_{k=0}^{n} h_k = \binom{n+1}{1} + 2 \binom{n+1}{2} + 12 \binom{n+1}{3} + 6\binom{n+1}{4} $$
The general expression of what we have calculated.
Theorem
Theorem 8.2.3 Assume that the sequence $h_0, h_1, h_2, \ldots, h_n, \ldots$ has a difference table whose 0 th diagonal equals $$ c_0, c_1, c_2, \ldots, c_p, 0,0, \ldots $$
Then $$ \sum_{k=0}^n h_k=c_0\left(\begin{array}{c} n+1 \ 1 \end{array}\right)+c_1\left(\begin{array}{c} n+1 \ 2 \end{array}\right)+\cdots+c_p\left(\begin{array}{c} n+1 \ p+1 \end{array}\right) $$
Proof is the same as our calculation above.
Next, we discuss the sequence $$ h_n = n^p $$ for some constant $p$.
Bell numbers
Theorem
If $p \geq 1$, then $$ B_p = \binom{p-1}{0} B_0 + \binom{p-1}{1}B_1 + \ldots + \binom{p-1}{p-1}B_{p-1} $$ Proof
Here is the construction:
There are $p$ elements in total, and some boxes.
- Fix the element $p$.
- Fix $t \in \set{0, \ldots, p-1}$ which chooses the number of elements in the box containning $p$.
Let $a_t = $ number of the choices of elements which are in the box with $p$, which equals $\binom{p-1}{t}$
It remains to partition $p-(t-1)$ elements into indistinguishable non-empty boxes $B_{p-t-1}$ ways. Writing out the relation we get:
Stirling number of the first kind
==…==