Erdos-Szekeres Theorem
Given $r, s$ any sequence of distinct real numbers with length at least $(r-1)(s-1)+1$ contains a monotonically increasing subsequence of length $r$ or a monotonically decreasing subsequece of length $s$.
That is, given the subsequence: $a_1, a_2, …, a_{(s-1)(r-1)+1}$, we can find:
- Indicies $i_1 < i_2 < …< i_r$ so that $a_{i1} < a_{i2} < …< a_{ir}$
OR
- Indicies $j_1 < j_2 < …< j_r$ so that $a_{j1} > a_{j2} > … > a_{jr}$
Example: $s = 3, r = 3$, Sequence: $10, 11, 7, 8$ has no such property.
E-S thm is best possible:
$\exists$ subsequence of length $(s-1)(r-1)$ so that $\not \exists$ increasing subsequence of length $r$ nor a decreasing subsequence of length $s$.
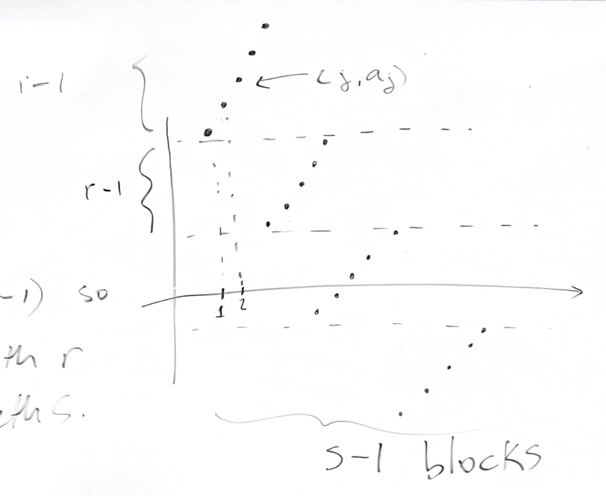
Proof
The subsequence: $a_1, a_2, …, a_{(s-1)(r-1)+1}$.
For each $i \in \set{1, …, (s-1)(r-1)+1}$, define a pair $(x_i, y_i)$ as follows:
$x_i = $ the length of the longest increasing subsequence $a_1, …, a_i$
$y_i = $ the length of the longest decreasing subsequence $a_1, …, a_i$
Example: subsequence $1, 4, 5, 2, 7, 3$
\begin{align*} (x_1, y_1) = (1, 1)\\ (x_2, y_2) = (2, 1)\\ (x_3, y_3) = (3, 1)\\ (x_4, y_4) = (3, 2)\\ \end{align*}
Claim 1: Let $i \in \set{1, …, (s-1)(r-1)}$
Then, either $x_{i+1} > x_i$ or $y_{i+1} > y_i$
Proof of claim 1:
Let $a_{j1}, a_{j2}, …, a_{jx_i}$ be the longest increasing subsequence in $a_1, …, a_i$, ending with $a_i$. So $a_{jx_i} = a_i$
Let $a_{t1}, a_{t2}, …, a_{ty_i}$ be the longest decreasing subsequence in $a_1, …, a_i$, ending with $a_i$. So $a_{ty_i} = a_i$
Two options:
- $a_{i+1} > a_i$, then it contributes to the increasing subsequence: $a_{j1}, …, a_{jx_i}, a_{i+1}$
- $a_{i+1} < a_i: a_{t_1} , …, a_{ty_i}, a_{i+1}$
Note that here, $a_{ty_i}$ and $a_{jx_i}$ are both equal to $a_i$
Claim 2: Let $i, j \in \set{1, …, (s-1)(r-1) + 1}$ with $i < j$. Then either $x_j > x_i$ or $y_j > x_i$. This gives us: $(x_i, y_i) \neq (x_j, y_j), \forall j \neq i$
Proof of claim 2:
Same notation as claim 1:
Let $a_{j1}, a_{j2}, …, a_{jx_i}$ be the longest increasing subsequence in $a_1, …, a_i$, ending with $a_i$. So $a_{jx_i} = a_i$
Let $a_{t1}, a_{t2}, …, a_{ty_i}$ be the longest decreasing subsequence in $a_1, …, a_i$, ending with $a_i$. So $a_{ty_i} = a_i$
There are two options:
- $a_j > a_i$. Then we can take $a_j, …, a_{jx_i}, a_j$ , which give us longer increasing $x_j > x_i$.
- $a_j < a_i$. Then we can take $a_t, …, a_{ty_i}, a_j$ , which give us longer decreasing $y_j > y_i$.
Now that the two claims are done, we can construct this box that contains $(r-1)(s-1)$ points. Then the extra one point in the 2D space gives us the fact that along one dimension, we have $s$ or $r$ points.
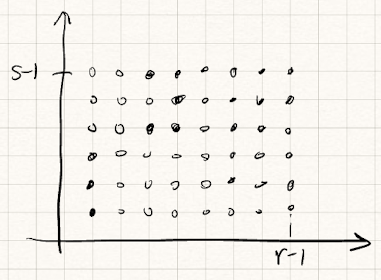
$\blacksquare$
Graph & Ramsey’s theories
Definition
A graph is an ordered pair $G = (V, E)$ comprising:
-
$V$, a set of vertices (also called nodes or points)
-
$E \subseteq \set{{x,y}: x,y \in V \text{ and } x \neq y}$, a set of edges (also called links or lines), which are unordered pairs of vertices.
Definition
-
A complete graph is a graph in which each pair of graph vertices is connected by an edge.
-
The complete graph with $n$ vertices is denoted by $K_n$.
Exercise
What is the number edges in $K_n$?
$\sum_{i=1}^{n-1} i$, or simply ${{n} \choose {2}}$
Theorem of Ramsey
Of six (or more) people, either there are three, each of pair of whom are acquainted, or there are three, each pair of whom are unaquainted.
In graph theory language: for any coloring of the edges of $K_6$ with red or blue, then there exists at least one monochromatic triangle $K_3$.
Question: How many ways to color $K_6$?
There are $e = {{6} \choose {2}} = 15$ edges, so the number of ways is $2^{15}$. It would be horrible to brute force checking all the possibilities.
Proof
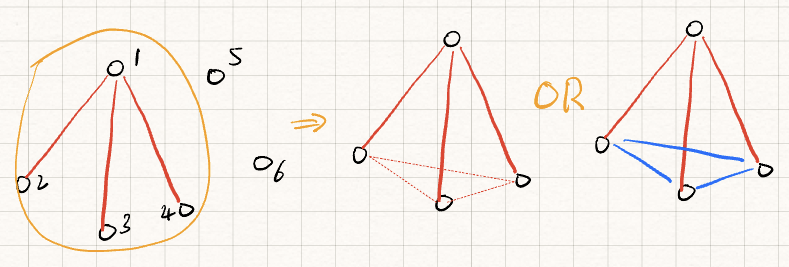
Labeling the graph verticies from 1 to 6.
There are 5 edges starting from 1. By pigeonhole principle, $\exists$ at least 3 edges of the same color. Then there are two cases:
- $\exists$ at least one red edge among the three verticies connected to 1, forming a red triangle.
- Otherwise, they are all blue, forming a blue triangle.
Notation:
$K_n \to K_s$ is the assertion that for any coloring of the edges of $K_n$ with red and blue, we can always find a monochromatic $K_s$.
$K_n \not \to K_s$ is the assertion that there exists a coloring of the edges of $K_n$ with red and blue with no monochromatic $K_s$.
Notation Ramsey number
Let $t \in \set{1, 2, 3,…}$. The Ramsey number $R(t)$ is the smallest value of $n$ such that $K_n \to K_t$.
Ramsey’s theorem
For every $k \in \mathbb{N}$, we have $R(k) \leq 4^k$.
Proof: $k$ is fixed
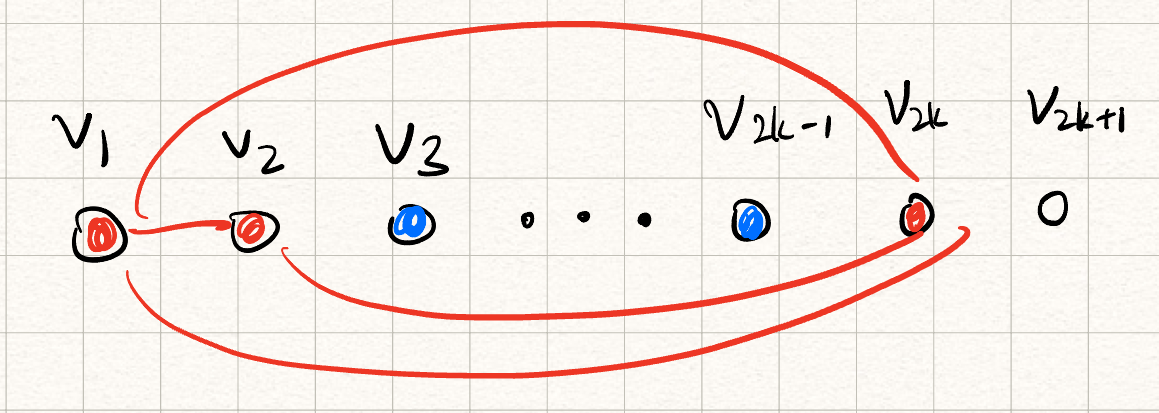
Take $n = 4^k$. Take one vertex, label it $v_1$. $v_1$ has $4^k - 1$ neighbors.
Note that either $|N_R(v_1)| \geq \frac{4^k}{2}$ or $|N_B(v_1)| \geq \frac{4^k}{2}$. (By pigeonhole)
$N_R(v_1) = \set{u:v_1u \text{ is red}}$
$N_B(v_1) = \set{u:v_1u \text{ is blue}}$
Step 1: Let us color $v_1$ blue if $|N_B(v_1)| \geq \frac{4^k}{2}$ and red otherwise.
Then, restrict our graph to $v_1 \cup N_{c(v_1)}(v_1)$.
Step 2: Take $v_2 \in N_{c(v_1)}(v_1)$. Color $v_2$ blue if $|N_B(v_2) \cap N_{c(v_1)}(v_1)| \geq \frac{4^k}{4}$, otherwise, color it red.
Because, by pigeonhole, either:
- $|N_B(v_2) \cap N_{c(v_1)}(v_1)|\geq \frac{4^k}{2} / 2$
- $|N_R(v_2) \cap N_{c(v_1)}(v_1)|\geq \frac{4^k}{2} / 2$
$\vdots$
Step $i+1$:
Take $v_{i+1} \in A_i = N_{c(v_1)}(v_1) \cap N_{c(v_2)}(v_2) \cap \cdots \cap N_{c(v_i)}(v_{i+1})$
Note that $|A_i| \geq \frac{4^k}{2^i}$. By pigeonhole, either:
- $|N_B(v_{i+1})| \geq \frac{4^k}{2^{i+1}}$
- $|N_R(v_{i+1})| \geq \frac{4^k}{2^{i+1}}$
Now when we get to $i = 2k-1, |A_{i-1}| \geq \frac{4^k}{2^{2k-1}} = 2$. So we can still color the vertex $v_{i+1}$
According to vertex coloring of $v_1, v_2, \cdots, v_{i}$, select majority color for $v_{i+1}$. This gives us a monochromatic $K_k$ by pigeonhole principle.
Reference:
https://lmattos.web.illinois.edu/math-413-lecture-log/, MATH 413, Leticia Dias Mattos