General Ramsey on normal graph
Notation General notation for Ramsey theory:
$K_n \to (K_s,K_t)$ is the assertion that for any coloring of the edges of $K_n$ with red and blue, we can always find a red $K_s$ or a blue $K_t$.
$K_n \not \to (K_s,K_t)$ is the assertion that there exists a coloring of the edges of $K_n$ with red and blue with no red $K_s$ nor blue $K_t$.
Notation Off-diagonal Ramsey numbers:
Let $s,t \in \set{1,2,3,\ldots}$. The Ramsey number $R(s,t)$ is the smallest value of $n$ such that $K_n \to (K_s,K_t)$.
$R(s, t) = \operatorname{min}\set{n : \forall c : E(K_n) \to \set{\text{red, blue}}, \exists \text{ red } K_s \text{ or blue }K_t}$
Observation
- $R(s, t) = R(t, s)$
- $R(2, t) = t$
Proof of observation 2:
$R(2, t) = \operatorname{min}\set{n : \forall c : E(K_n) \to \set{\text{red, blue}}, \exists \text{ red } K_2 \text{ or blue }K_t}$
Need to show two things:
- $\exists c : E(K_{t-1}) \to \set{\text{red, blue}} \text{ s.t. } \not \exists \text{ red } K_2 \text{ or blue }K_t$. This holds since we have at most a blue $K_{t-1}$, the two coloring we want are both not satisfied. This property gives us $R(2, t) \geq t$.
- $\forall c : E(K_t) \to \text{red, blue, }\exists \text{ red } K_2 \text{ or blue }K_t$. This holds since we either have one red edge, then done. Or all the edges are blue, then blue $K_t$, also done. This property gives us $R(2, t) \leq t$.
Theorem
For all $s, t \in \mathbb{N}$, we have $R(s, t) \leq R(s-1, t) + R(s, t-1)$.
⚠️ Understanding this proof is important… As we have a more generalized version of Ramsey’s theorem below, which has a similar proof. (In a same structure but using much more complicate notations.)
Proof
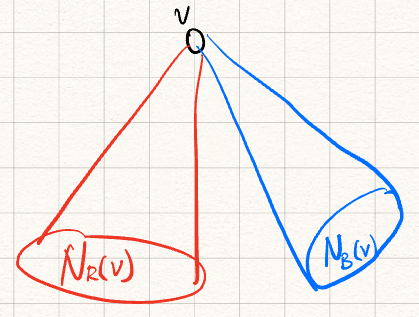
Suppose you have a complete graph $K_n, n = R(s-1, t) + R(s, t-1)$. Now, fix the coloring $c : E(K_n) \to \set{\text{red, blue}}$.
Goal: to show that $\exists $ red $K_s$ or blue $K_t$.
Take a vertex $v$. Consider their red and blue neighbours of this $v$. Denote $N_R(v), N_B(v)$. We cannot have at the same time that:
- $|N_R(v) \leq R(s-1,t) - 1|$
- $|N_B(v) \leq R(s,t-1) - 1|$
This is because, by contradiction, $n = N_R(v) + N_B(v) + 1 \leq n-1$.
Two cases:
- $|N_R(v)| \geq R(s-1, t)$
Inside $N_R(v)$, we can find $K_{s-1}$ red or $K_t$ blue. If $K_t$ blue, done. If $K_{s-1}$ red, also done since we have this $v$ here, adding an extra 1 to $K_{s-1}$.
- $|N_B(v)| \geq R(s, t-1)$. This has a similar argument.
Corollary
For all $s, t \in \mathbb{N}$, we have $R(s, t) \leq {{s+t-2} \choose {s-1}}$
Proof
Two observations:
- $R(2, t) = t$
- $R(s, t) \leq R(s-1, t) + R(s, t-1)$.
By induction on $s+t$
Base case: $s+t = 4$.
$R(2, 2) \leq {{2} \choose {1}} = 2$ by (1)
$R(1, 3) \leq {{2} \choose {0}} = 1$
IH: Assume that it is true for $R(s-1, t)$ and $R(s, t-1)$. Let us show that this is true for $R(s, t)$.
\begin{align*} R(s, t) \leq R(s-1, t) + R(s, t-1) \\ \leq {{s+t-3} \choose {s-2}} + {{s+t-3} \choose {s-1}}\\ = {{s+t-2} \choose {s-1}} &&\text{by Pascal} \end{align*}
Application: new proof for $R(t) \leq 4^t$: $$ R(t, t) \leq {{2t-2} \choose {t-1}} \leq 2^{2t-2} = \frac{4^t}{4} $$
Ramsey for many colors on normal graph
$K_n \to (K_{t_1},K_{t_2},\ldots,K_{t_k})$ is the assertion that for any coloring $c:E(K_n)\to \set{1,2,\ldots,k}$ of the edges of $K_n$, there exists an $i$ so that we have a $i$-colored copy of $K_{t_i}$ under $c$.
Reminder: $E$ here is the notation for edges
Notation Generalized Ramsey numbers:
The Ramsey number $R(t_1,\ldots,t_k)$ is the smallest value of $n$ such that $K_n \to (K_{t_1},\ldots,K_{t_k})$.
Ramsey’s Theorem
For any $k \in \mathbb{N}$ and any $t_1, t_2, \ldots, t_k \in \mathbb{N}$, we have
$$ R(t_1, \ldots, t_k) \leq \infty $$
Consider $R(t_1, t_2, t_3) \leq R(R(t_1, t_2), t_3) < \infty$
We want to prove the first inequality as the second one is trivial by definition.
Proof
Let $n \geq (R(R(t_1, t_2), t_3))$
Let $c : E(K_n) \to \set{\text{red, blue, green}}$ by any coloring. First, identify the red and blue color as black.
Goal: to find red $K_{t_1}$ or blue $K_{t_2}$ or green $K_{t_3}$.
As $R(s, t) < \infty \implies R(R(t_1, t_2), t_3) < \infty$
$\implies$ we find a black clique of size $R(t_1, t_2)$ in $K_n$ under $c$, or a green clique of size $K_{t_3}$.
Case 1: We find the green $K_{t_3}$, we are done.
Case 2: We find a black $K_{R(t_1, t_2)}$. In this graph, all edges are red or blue. We are garenteed to find $K_{t_1}$ red or $K_{t_2}$ blue.
NOW, more general Ramsey on Hypergraph🙃
Instead of coloring edges(pair of vertices, they are sets of size two), we can color sets! (How cool is that 🙃🙃🙃)
Definition Hypergraph
A hypergraph is a pair $(V, E)$ where $V$ is a set of vertices and $E$ is a collection of subset of $V$.

Then the maximum number of hyperedges is just $|P(V) - 1|$. (empty set is not included)
Notation $r$-uniform hypergraph
Let $r \in \mathbb{N}$. We say that a hypergraph $\mathcal{H}=(V,E)$ is $r$-uniform if all its hyperedges have $r$ vertices.
Definition Complete hypergraph
Let $\mathcal{H} = (V, E)$ be an $r$-uniform hypergraph on $n$ vertices. We say that $\mathcal{H}$ is a complete hypergraph if every subset of $V$ of size $r$ is a hypergraph of $\mathcal{H}$. That is: $$ E = \set{A : A \subseteq V \text{ and } |A| = r} $$ Observe: $|E(\mathcal{H})| = {{n} \choose {r}}$
Notation $K_n^r$ denotes the complete $r$-uniform hypergraph.
Notation Ramsey for hypergraphs
$K_n^r \to (K_{t_1}^r,K_{t_2}^r,\ldots,K_{t_k}^r)$ is the assertion that for any coloring $c:E(K_n)\to \set{1,2,\ldots,k}$ of the hyperedges of $K_n^r$, there exists an $i$ so that we have a $i$-colored copy of $K^r_{t_i}$ under $c$.
Notation Ramsey numbers for hypergraphs
The Ramsey number $R_r(t_1,\ldots,t_k)$ is the smallest value of $n$ such that $K_n^r \to (K_{t_1}^r,\ldots,K_{t_k}^r)$.
Observation
$R_3(3, 10) = 10$
$R_r(r, t) = t$
All of these are the analogies of Ramsey’s theories on normal graph with many colors.
Ramsey’s theorem for hypergraph
For any $r, k \in \mathbb{N}$ and any $t_1, …, t_k \in \mathbb{N}$ we have $$ R_r(t_1, \ldots, t_k) \leq \infty $$ Proof
Induction on $r$ and $t_1 + … + t_k$
Question: What should be the degree of a vertex so that in its neighbourhood we guarentee (1) $K_{t_1}^r$ 1-colored or (2)$K_{t_2}^r$ 2-colored or …
Claim:
\begin{align*} R_r(t_1,t_2, t_3) &\leq R_{r-1}(R(t_1-1, t_2, t_3)) \\ &+ R_{r-1}(R(t_1, t_2-1, t_3)) \\ &+ R_{r-1}(R(t_1, t_2, t_3-1)) \end{align*}
Call the right side $n$.
Fix any coloring $c : E(K_n^r) \to \set{\text{red, blue, green}}$
Goal: to find red $K_{t_1}^r$ or blue $K_{t_2}^r$ or green $K_{t_3}^r$
By pigeonhole principle:
Let’s define the coloring:
$c’ : E(K_{n-1}^{r-1}) \to \set{\text{red, blue, green}}$ as follows:
- $c’(e) = $ $c(v \cup e)$
==The detailed proof goes in the homework…==
Now, there is one interesting application of this Ramsey’s theorem for hypergraph.
The happy ending problem
Let $A$ be a set of $n$ points in $\mathbb{R}^2$ such that no three points of $A$ are co-linear. If $n$ is sufficiently large, then $A$ contains $k$ points forming a convex $k$-gon.
Solved by Erdos-Szekeres.
Definition The definition of a convex polygon is a bit complicated. But they have this property:
In a convex polygon, all interior angles are less than or equal to 180 degrees, while in a strictly convex polygon all interior angles are strictly less than 180 degrees. (https://en.wikipedia.org/wiki/Convex_polygon)
Some simple cases:
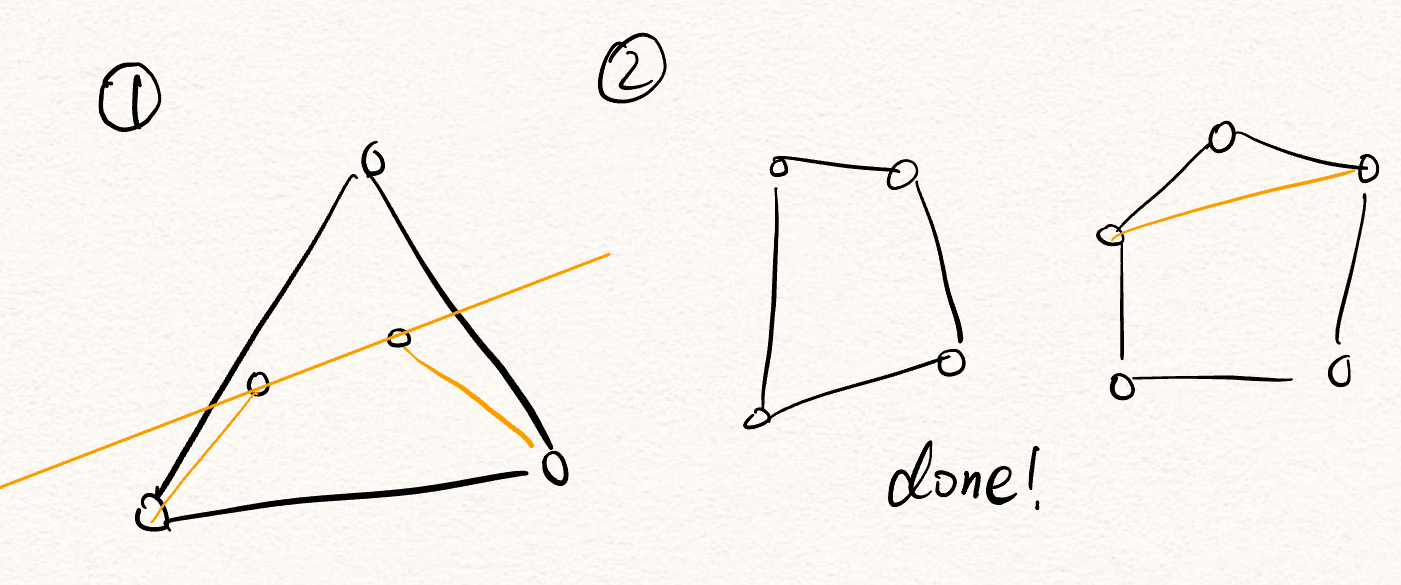
Question: How many points in general position guarantee a convex 3-gon? THREE!
How many points in general position guarantee a convex 4-gon? Four is not enough. Consider an arrow like 4-gon.
Suppose we have 5 points in general position (g.p. means no 3 are colinear). Whenever we have a convex 4-gon or 5-gon, we are done. Otherwise, in case (1), draw a line inside the triangle, it crosses two edges. We can see that the two any two points on the line, together with other two points, will form a 4-gon. (I don’t know how to argue this using a formal geometry proof, but the intuition should be similar to this.)
General Proof
Consider any set of $n = R_4(k,k)$ points in general position: $p_1, \ldots, p_n$.
We define a coloring of $K_n^4$ as follows:
- Color $p_1, p_2, p_3, p_4$ blue if these points are in convex position.
- Color them red if they are not covex.
Then Ramsey’s Theorem tells us that: $\exists$ monochromatic $K_k^4$.
Question: Can all hyperedges be red? What happenwith 5 points in general position?
$K \geq 5 \implies \exists$ convex 4-gon $\implies$ blue edges $\implies$ the monochromatic $k$-clique is blue!
Conclusion: we can find $k$ points $p_1, \ldots, p_k$ so that every 4-points are in convex position.
BUT, what’s next? Hint: loook at the convex hull.
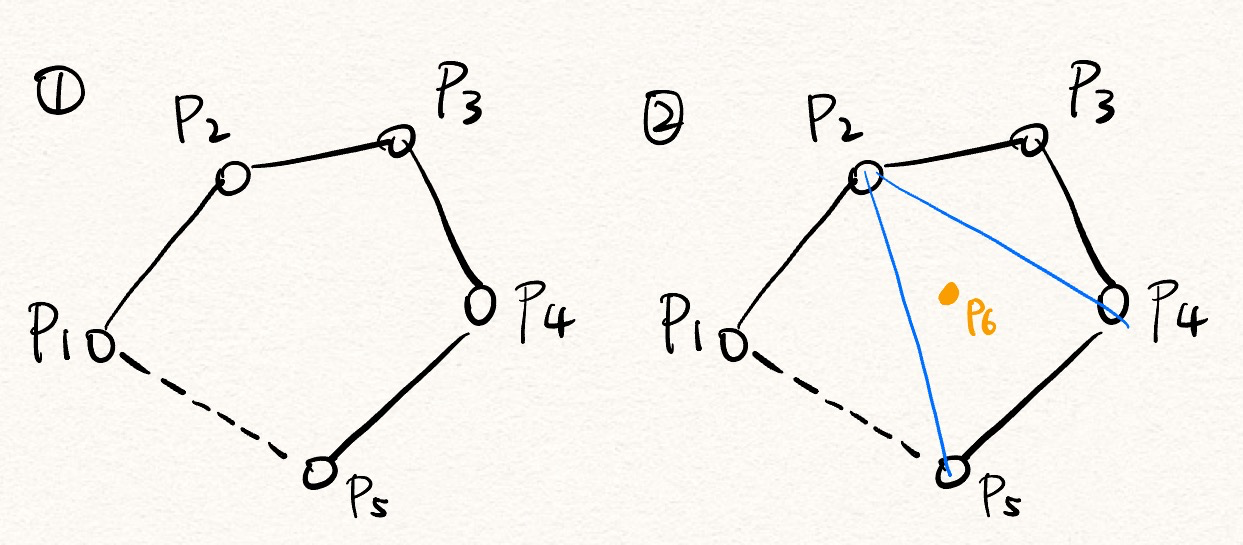
Case 1: If we find all these $k$ points forms a convex $k$-gon (case 1), then we are happy.
Otherwise, in case 2: Choose one vertex, and draw lines to other verticies. If there is a point “inside”, it must be inside one of the triangles created. Then those four points forms a non-convex 4-gon, which contradicts our conclution. Then only case 1 exists. $\blacksquare$
Wish you a good dream without Ramsey😴
Reference:
https://lmattos.web.illinois.edu/math-413-lecture-log/, MATH 413, Leticia Dias Mattos