Pasting Images
Method 1 — Cut and paste the images.
-
Feathering
- Gives a smoother transition. But that’s all…
-
Alpha composting
- Output = foreground $\times$ mask + background $\times$ (1 $-$ mask). We can also use alpha compositing together with the feathering — simply bluring the mask will give us a good feathering. This method is also good for multilayer processing, which allwos the compositing to be more complicated.
Method 2 — Pyramid Blending
- At low frequencies, blend slowly
- At high frequencies, blend quickly
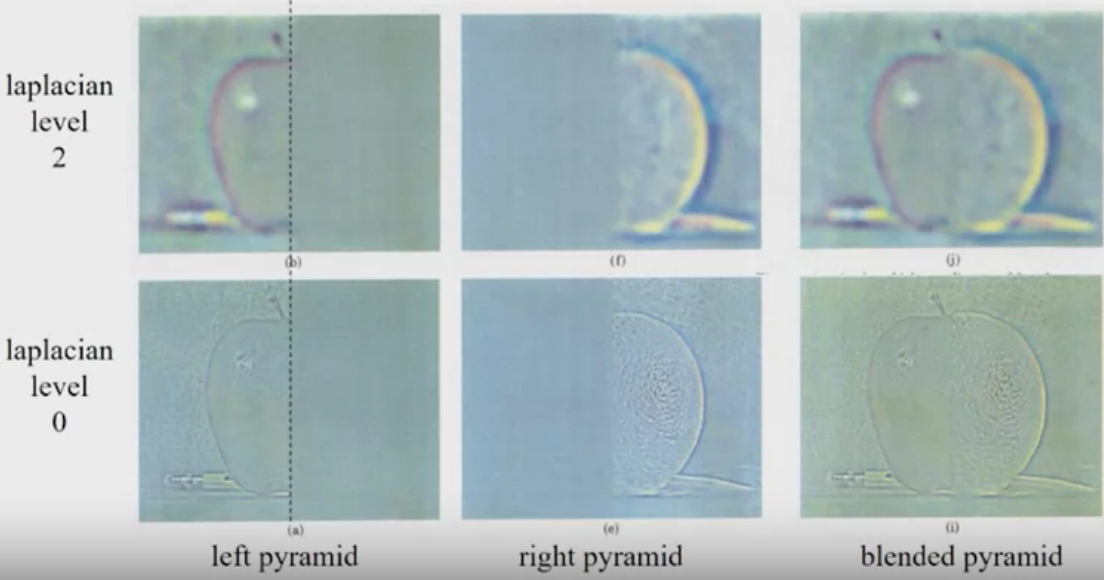

Implementation:
- Build Laplacian pyramids for each image
- Build a Gaussian pyramid of region mask
- Blend each level of pyramid using region mask from the same level
$$ L_{12}^i=L_1^i \cdot R^i+L_2^i \cdot\left(1-R^i\right) $$
- Collapse the pyramid to get the final blended image
Method 3: Poisson Blending
A good blend should preserve gradient of source region withough changing the background
Treat pixels as variables to be solved
- Minimize squared difference between gradients of foreground region and gradients of target region
- Keep background pixels constant
$$ \mathbf{v}=\underset{\mathbf{v}}{\operatorname{argmin}} \sum_{i \in S, j \in N_i \cap S}\left(\left(v_i-v_j\right)-\left(s_i-s_j\right)\right)^2+\sum_{i \in S, j \in N_i \cap \neg S}\left(\left(v_i-t_j\right)-\left(s_i-s_j\right)\right)^2 $$

We want to put source image on the background image. The result is called “target image”. So, inside the pasted regeion, we want to make the gradient similar to the source image. But in the edge of our pasted regeion, we also want to make the transformation smaller. We can then use a least square method to solve for a vector $\vec v$ to minimize the error.
In this example here, we have:
$v_3 - v_1 \approx s_{10} - s_{6} $
$v_1 - t_2 \approx s_6 - s_2$
Note that this method doesn’t care color, so putting a bear in a pool of water will make the bear turn green.

Method 4: Blending with Mixed Gradients
Use fourground or background gradient with larger magnitude as the guiding gradient. Since the larger gradient is always percieved, it is more likely to have the result of “writing something on the wall” instead of “sticking an printed image on the wall”.
Reference
CS445 Derek Hoiem: https://courses.engr.illinois.edu/cs445/fa2023/