How do you view the world
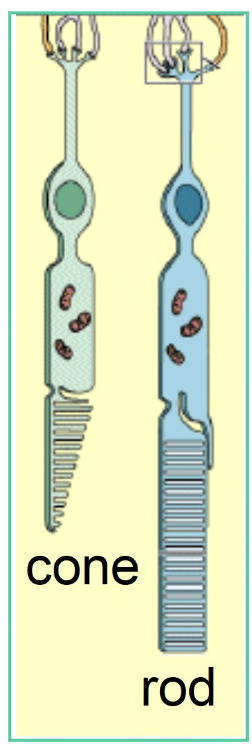
Cones: cone-shaped, less sensitive, operate in high light, color vision
Rods: rod-shaped, highly sensitive, operate at night, gray-scale vision, slower to respond
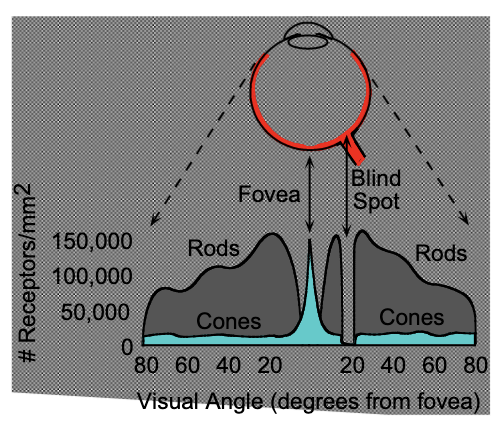
Observation In a clear night, there are more stars off-center. This is because you have more rods in the middle, while more cones elsewhere.
How to express colors?
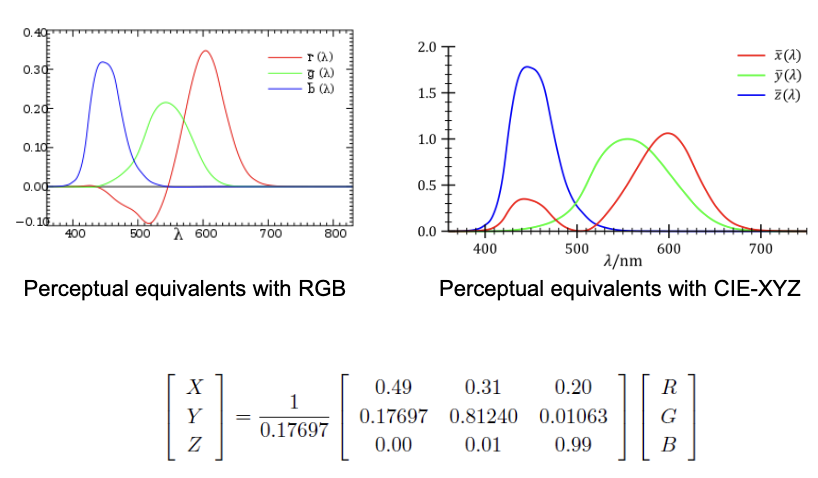
Basically, the most intuitive expression is the RGB color space. But it is not a linear color space. We perfer expressing using CIE-XYZ color space, which makes the calculation much easier.

How is light reflected from a surface?
Lambertian surface
- Some light is absorbed
- The rests are reflected in all direction (diffuse reflection. Think of how you view a piece of white paper)
Diffuce reflection, the intensity does depend on illumination angle. $$ I(x) = \rho(x)(S\cdot N(x)) $$
where $\rho$ is albedo, $S$ is the directional source, $N$ is the surface normal, $I$ is the image complexity.
However, perceived intensity does not depend on viewer angle
Specular Reflection, consider mirror.
Most surfaces have these two kinds of reflection. We also have more complicated reflections and refractions.
Color spaces
CIE-XYZ
As above.
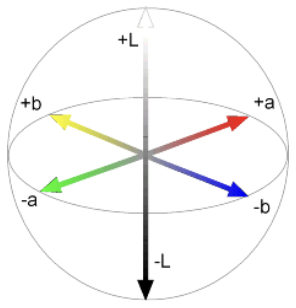
CIE L*a*b*
This color space sepearates the luminance and chrominance. It turns out that, people gains more information from the luminance channel.
HSV
Hue, Saturation, Value
YCbCr
This is good for fast computation and easier compression.
Enhancement
Color balancing: White balance
Simple idea: multiply R, G, and B values by separate constants. $$ \left[\begin{array}{l} \tilde{r} \ \tilde{g} \ \tilde{b} \end{array}\right]=\left[\begin{array}{ccc} \alpha_r & 0 & 0 \ 0 & \alpha_g & 0 \ 0 & 0 & \alpha_b \end{array}\right]\left[\begin{array}{l} r \ g \ b \end{array}\right] $$
- Gray world assumption.
Calculate:
red_avg as the mean of all the red channel
avg = (red_avg + green_avg + blue_avg) / 3
Choose $\alpha_r$ by calculating avg/red_avg
- Use a natural color(white, gray) regeion for calibration.
https://stackoverflow.com/questions/54470148/white-balance-a-photo-from-a-known-point gave me an idea:
Given an natrual color point, calculate:
- The luminance of the given point by
(choice_r + choice_g + choice_b) / 3 - Calculate $\alpha_r$ by
choice_lum/choice_r
Gamma adjustment
$$ i_{\text {out }}=i_{\text {in }}^\gamma $$
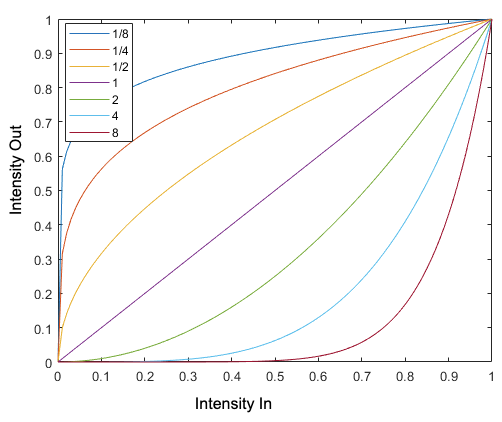
Note that the input range should be in 0 to 1.
Historgram equalization
Basic idea: reassign values so that the number of pixels with each value is more evenly distributed. So the histogram should look much smoother instead of having high hills and low valleys.
There is an algorithm for global histogram equalization.
Goal: Given image with pixel values $0 \leq p j \leq 255, j=0 . . N$ specify function $\mathrm{f}(i)$ that remaps pixel values, so that the new values are more broadly distributed
- Compute cumulative histogram: $c(i), i=0 . .255$ $$ h(i)=\sum_{j \in \text { pixels }} \mathbf{1}\left(p_j==i\right), c(i)=c(i-1)+h(i) $$
- $\mathrm{f}(i)=\alpha \cdot \frac{c(i)}{N} \cdot 255+(1-\alpha) \cdot i$
- Blends between original image and image with equalized histogram
Reference
CS445 Derek Hoiem: https://courses.engr.illinois.edu/cs445/fa2023/